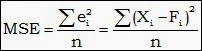FORECASTING (PERAMALAN)
Ajeng sri novia
3 MKS A “1123070003”
Peramalan merupakan
aktivitas fungsi bisnis yang memperkirakan penjualan dan penggunaan produk
sehingga produk-produk itu dapat dibuat dalam kuantitas yang tepat. Peramalan
merupakan dugaan terhadap permintaan yang akan datang berdasarkan pada beberapa
variabel peramal, sering berdasarkan data deret waktu historis. Peramalan
menggunakan teknik-teknik peramalan yang bersifat formal maupun informal
(Gaspersz, 1998).
Kegiatan peramalan
merupakan bagian integral dari pengambilan keputusan manajemen. Peramalan
mengurangi ketergantungan pada hal-hal yang belum pasti (intuitif). Peramalan
memiliki sifat saling ketergantungan antar divisi atau bagian. Kesalahan dalam
proyeksi penjualan akan mempengaruhi pada ramalan anggaran, pengeluaran
operasi, arus kas, persediaan, dan sebagainya. Dua hal pokok yang harus
diperhatikan dalam proses peramalan yang akurat dan bermanfaat (Makridakis,
1999):
- Pengumpulan data yang relevan berupa informasi yang dapat menghasilkan peramalan yang akurat.
- Pemilihan teknik peramalan yang tepat yang akan memanfaatkan informasi data yang diperoleh semaksimal mungkin.
Terdapat dua
pendekatan untuk melakukan peramalan yaitu dengan pendekatan kualitatif dan
pendekatan kuantitatif. Metode peramalan kualitatif digunakan ketika data
historis tidak tersedia. Metode peramalan kualitatif adalah metode subyektif
(intuitif). Metode ini didasarkan pada informasi kualitatif. Dasar informasi
ini dapat memprediksi kejadian-kejadian di masa yang akan datang. Keakuratan
dari metode ini sangat subjektif (Materi Statistika, UGM).
Metode peramalan
kuantitatif dapat dibagi menjadi dua tipe, causal dan time series.
Metode peramalan causal meliputi faktor-faktor yang berhubungan dengan
variabel yang diprediksi seperti analisis regresi. Peramalan time series
merupakan metode kuantitatif untuk menganalisis data masa lampau yang telah
dikumpulkan secara teratur menggunakan teknik yang tepat. Hasilnya dapat
dijadikan acuan untuk peramalan nilai di masa yang akan datang (Makridakis,
1999).
Model deret berkala
dapat digunakan dengan mudah untuk meramal, sedang model kausal lebih berhasil
untuk pengambilan keputusan dan kebijakan. Peramalan harus mendasarkan
analisisnya pada pola data yang ada. Empat pola data yang lazim ditemui dalam
peramalan (Materi Statistika, UGM):
1. Pola Horizontal
2. Pola Musiman
Pola musiman terjadi
bila nilai data dipengaruhi oleh faktor musiman (misalnya kuartal tahun
tertentu, bulanan atau hari-hari pada minggu tertentu). Struktur datanya dapat
digambarkan sebagai berikut ini.
3. Pola Siklis
Pola ini terjadi bila
data dipengaruhi oleh fluktuasi ekonomi jangka panjang seperti yang berhubungan
dengan siklus bisnis. Struktur datanya dapat digambarkan sebagai berikut.
4. Pola Trend
Pola Trend terjadi
bila ada kenaikan atau penurunan sekuler jangka panjang dalam data. Struktur
datanya dapat digambarkan sebagai berikut.
Forecasting adalah peramalan atau perkiraan mengenai sesuatu yang belum
terjadi. Ramalan yang dilakukan pada umumnya akan berdasarkan data yang
terdapat di masa lampau yang dianalisis dengan mengunakan metode-metode
tertentu. Forecasting diupayakan dibuat dapat meminimumkan pengaruh
ketidakpastian tersebut, dengan kata lainbertujuan mendapatkan ramalanyang bisa
meminimumkan kesalahan meramal (forecast error) yang biasanya diukur
dengan Mean Absolute Deviation, Absolute Error, dan sebagainya.
Peramalan merupakan alat bantu yang sangat penting dalam perencanaan yang
efektif dan efisien (Subagyo, 1986).
Peramalan permintaan
memiliki karakteristik tertentu yang berlaku secara umum. Karakteristik ini
harus diperhatikan untuk menilai hasil suatu proses peramalan permintaan dan
metode peramalan yang digunakan. Karakteristik peramalan yaitu faktor penyebab
yang berlaku di masa lalu diasumsikan akan berlaku juga di masa yang akan
datang, dan peramalan tak pernah sempurna, permintaan aktual selalu berbeda
dengan permintaan yang diramalkan (Baroto, 2002).
Penggunaan berbagai
model peramalan akan memberikan nilai ramalan yang berbeda dan derajat dari
galat ramalan (forecast error) yang berbeda pula. Seni dalam melakukan
peramalan adalah memilih model peramalan terbaik yang mampu mengidentifikasi
dan menanggapi pola aktivitas historis dari data. Model-model peramalan dapat
dikelompokan ke dalam dua kelompok utama, yaitu metode kualitatif dan metode
kuantitatif. Metode kuantitatif dikelompokkan ke dalam dua kelompok utama,
yaitu intrinsik dan ekstrinsik.
Metode kualitatif
ditujukan untuk peramalan terhadap produk baru, pasar baru, proses baru,
perubahan sosial dari masyarakat, perubahan teknologi, atau penyesuaian
terhadap ramalan-ramalan berdasarkan metode kuantitatif.
Metode Peramalan:
·
Model kuantitatif
intrinsik sering disebut sebagai model-model deret waktu (Time Series model).
Model deret waktu yang populer dan umum diterapkan dalam peramalan permintaan
adalah rata-rata bergerak (Moving Averages), pemulusan eksponensial (Exponential
Smoothing), dan proyeksi kecenderungan (Trend Projection). Model
kuantitatif ekstrinsik sering disebut juga sebagai model kausal, dan yang umum
digunakan adalah model regresi (Regression Causal model) (Gaspersz,
1998).
1. Weight Moving Averages (WMA)
Model rata-rata
bergerak menggunakan sejumlah data aktual permintaan yang baru untuk
membangkitkan nilai ramalan untuk permintaan di masa yang akan datang. metode
rata-rata bergerak akan efektif diterapkan apabila permintaan pasar terhadap
produk diasumsikan stabil sepanjang waktu. Metode rata-rata bergerak terdapat
dua jenis, rata-rata bergerak tidak berbobot (Unweight Moving Averages)
dan rata-rata bobot bergerak (Weight Moving Averages). Model rata-rata
bobot bergerak lebih responsif terhadap perubahan karena data dari periode yang
baru biasanya diberi bobot lebih besar. Rumus rata-rata bobot bergerak yaitu
sebagai berikut.
2. Single Exponential
Smoothing (SES)
Pola data yang tidak
stabil atau perubahannya besar dan bergejolak umumnya menggunakan model pemulusan
eksponensial (Exponential Smoothing Models). Metode Single
Exponential Smoothing lebih cocok digunakan untuk meramalkan hal-hal yang
fluktuasinya secara acak (tidak teratur). Peramalan menggunakan model pemulusan
eksponensial rumusnya adalah sebagai berikut.
Permasalahan umum yang
dihadapi apabila menggunakan model pemulusan eksponensial adalah memilih
konstanta pemulusan (α) yang diperirakan tepat. Nilai konstanta pemulusan
dipilih di antara 0 dan 1 karena berlaku 0 < α < 1. Apabila pola historis
dari data aktual permintaan sangat bergejolak atau tidak stabil dari waktu ke
waktu, nilai α yang dipilih adalah yang mendekati 1. Pola historis dari data
aktual permintaan tidak berfluktuasi atau relatif stabil dari waktu ke waktu, α
yang dipilih adalah yang nilainya mendekati nol (Gaspersz, 1998).
3. Regresi Linier
Model analisis Regresi
Linier adalah suatu metode populer untuk berbagai macam permasalahan. Menurut
Harding (1974) dua variabel yang digunakan, variabel x dan variabel y,
diasumsikan memiliki kaitan satu sama lain dan bersifat linier. Rumus
perhitungan Regresi Linier yaitu sebagai berikut.
Y = hasil peramalan
n = periode
a = perpotongan dengan
sumbu tegak
b = menyatakan slope
atau kemiringan garis regresi
Ukuran Akurasi Peramalan:
Model-model peramalan
yang dilakukan kemudian divalidasi menggunakan sejumlah indikator.
Indikator-indikator yang umum digunakan adalah rata-rata penyimpangan absolut (Mean
Absolute Deviation), rata-rata kuadrat terkecil (Mean Square Error),
rata-rata persentase kesalahan absolut (Mean Absolute Percentage Error),
validasi peramalan (Tracking Signal), dan pengujian kestabilan (Moving
Range).
1. Mean Absolute Deviation
(MAD)
Metode untuk
mengevaluasi metode peramalan menggunakan jumlah dari kesalahan-kesalahan yang
absolut. Mean Absolute Deviation (MAD) mengukur ketepatan ramalan
dengan merata-rata kesalahan dugaan (nilai absolut masing-masing kesalahan).
MAD berguna ketika mengukur kesalahan ramalan dalam unit yang sama sebagai
deret asli. Nilai MAD dapat dihitung dengan menggunakan rumus sebegai berikut.
2. Mean Square Error (MSE)
Mean Squared Error
(MSE) adalah metode lain untuk mengevaluasi metode peramalan. Masing-masing
kesalahan atau sisa dikuadratkan. Kemudian dijumlahkan dan ditambahkan dengan
jumlah observasi. Pendekatan ini mengatur kesalahan peramalan yang besar karena
kesalahan-kesalahan itu dikuadratkan. Metode itu menghasilkan
kesalahan-kesalahan sedang yang kemungkinan lebih baik untuk kesalahan kecil,
tetapi kadang menghasilkan perbedaan yang besar.
3. Mean Absolute
Percentage Error (MAPE)
Mean Absolute
Percentage Error (MAPE) dihitung dengan
menggunakan kesalahan absolut pada tiap periode dibagi dengan nilai observasi
yang nyata untuk periode itu. Kemudian, merata-rata kesalahan persentase absolut
tersebut. Pendekatan ini berguna ketika ukuran atau besar variabel ramalan itu
penting dalam mengevaluasi ketepatan ramalan. MAPE mengindikasi seberapa besar
kesalahan dalam meramal yang dibandingkan dengan nilai nyata.
4. Tracking Signal
Validasi peramalan
dilakukan dengan Tracking Signal. Tracking Signal adalah suatu
ukuran bagaimana baiknya suatu peramalan memperkirakan nilai-nilai aktual.
Nilai Tracking Signal dapat dihitung dengan menggunakan rumus sebegai
berikut.
Tracking signal yang positif menunjukan bahwa nilai aktual permintaan lebih
besar daripada ramalan, sedangkan tracking signal yang negatif berarti
nilai aktual permintaan lebih kecil daripada ramalan. Tracking signal
disebut baik apabila memiliki RSFE yang rendah, dan mempunyai positive error
yang sama banyak atau seimbang dengan negative error, sehingga pusat
dari tracking signal mendekati nol. Tracking signal yang telah
dihitung dapat dibuat peta kontrol untuk melihat kelayakkan data di dalam batas
kontrol atas dan batas kontrol bawah.
5. Moving Range (MR)
Peta Moving Range
dirancang untuk membandingkan nilai permintaan aktual dengan nilai peramalan.
Data permintaan aktual dibandingkan dengan nilai peramal pada periode yang
sama. Peta tersebut dikembangkan ke periode yang akan datang hingga dapat
dibandingkan data peramalan dengan permintaan aktual. Peta Moving Range
digunakan untuk pengujian kestabilan sistem sebab-akibat yang mempengaruhi
permintaan. Rumus perhitungan peta Moving Range adalah sebagai berikut.
Jika ditemukan satu
titik yang berada diluar batas kendali pada saat peramalan diverifikasi maka
harus ditentukan apakah data harus diabaikan atau mencari peramal baru. Jika
ditemukan sebuah titik berada diluar batas kendali maka harus diselidiki
penyebabnya. Penemuan itu mungkin saja membutuhkan penyelidikan yang ekstensif.
Jika semua titik berada di dalam batas kendali, diasumsikan bahwa peramalan
permintaan yang dihasilkan telah cukup baik. Jika terdapat titik yang berada di
luar batas kendali, jelas bahwa peramalan yang didapat kurang baik dan harus
direvisi (Gaspersz, 1998).
Kegunaan peta Moving
Range ialah untuk melakukan verifikasi hasil peramalan least square
terdahulu. Jika peta Moving Range menunjukkan keadaan diluar kriteria
kendali. Hal ini berarti terdapat data yang tidak berasal dari sistem
sebab-akibat yang sama dan harus dibuang maka peramalan pun harus diulangi
lagi.